Note

Go to the end to download the full example code.

GroMo tutorial#

This is a minimal example of how to use GroMo. We will illustrate the use off GroMo to find a one hidden layer neural network (NN) that approximates the function \(f(x) = \sin(x)\) on the interval \([0, 2\pi]\).

Imports#

  • We use torch as the backend for all the computations.

  • matplotlib is used for plotting the results.

  • global_device is used to automatically select the device (CPU or GPU) for computations.

  • LinearGrowingModule is the main class of GroMo, which implements fully connected growing modules.

  • SinDataLoader is a custom data loader that generates the training data for the sine function.

  • train is exactly like a standard PyTorch training loop

  • evaluate is exactly like a standard PyTorch evaluation loop

Then we define plt_model to visualize the model.

import matplotlib.pyplot as plt
import torch
from helpers.auxilliary_functions import SinDataloader, evaluate_model, train

from gromo.modules.linear_growing_module import LinearGrowingModule
from gromo.utils.utils import global_device


global_device()

device(type='cpu')

def plt_model(model: torch.nn.Module, fig: "plt.axes._axes.Axes") -> None:
    """
    Plot the model's predictions and the true function.

    Parameters
    ----------
    model : torch.nn.Module
        The model to plot.
    fig : plt.axes._axes.Axes
        The figure to plot on.

    Returns
    -------
    None
    """
    x = torch.linspace(0, 2 * torch.pi, 1000, device=global_device()).view(-1, 1)
    y = torch.sin(x)
    y_pred = model(x)
    fig.plot(x.cpu().numpy(), y.cpu().numpy(), label="sin")
    fig.plot(x.cpu().numpy(), y_pred.cpu().detach().numpy(), label="Predicted")
    fig.legend()
    fig.set_xlabel("x")
    fig.yaxis.set_label_position("right")
    fig.set_ylabel("sin(x)")

data = SinDataloader(nb_sample=10, batch_size=100)
loss_function = torch.nn.MSELoss()

1. Define the model#

first_layer = LinearGrowingModule(
    in_features=1,
    out_features=2,
    use_bias=True,
    post_layer_function=torch.nn.GELU(),
    name="first_layer",
)

second_layer = LinearGrowingModule(
    in_features=2,
    out_features=1,
    use_bias=True,
    name="second_layer",
    previous_module=first_layer,
)

growing_net = torch.nn.Sequential(
    first_layer,
    second_layer,
)

growing_net = growing_net.to(global_device())

print(growing_net)

Sequential(
  (0): LinearGrowingModule(LinearGrowingModule(first_layer))(in_features=1, out_features=2, use_bias=True)
  (1): LinearGrowingModule(LinearGrowingModule(second_layer))(in_features=2, out_features=1, use_bias=True)
)

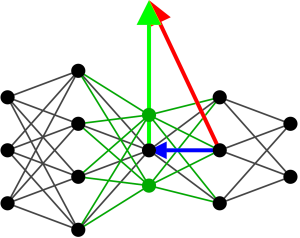
Here we define the following network:

\[\begin{split}x \mapsto \begin{bmatrix} z_1 \\ z_2 \end{bmatrix} \mapsto \begin{bmatrix} \sigma(z_1) \\ \sigma(z_2) \end{bmatrix} \mapsto y\end{split}\]

where \(\sigma\) is the activation function, \(z_1\) and \(z_2\) are the outputs of the first fully connected layer, and \(y\) is the output of the whole network.

Note that the activation function is included in the first ``LinearGrowingModule`` layer, this allow to easily access the intermediate results both before and after the activation function.

Note also that the second layer is linked to the first one by previous_module=first_layer. This allows extending the input of the second layer and let it grow with the first layer.

2. Use it like a normal model#

l2_err = evaluate_model(growing_net, data, loss_function)[0]
print(f"Initial error: {l2_err:.2e}")
fig, ax = plt.subplots(1, 1, figsize=(10, 5))
plt_model(growing_net, ax)
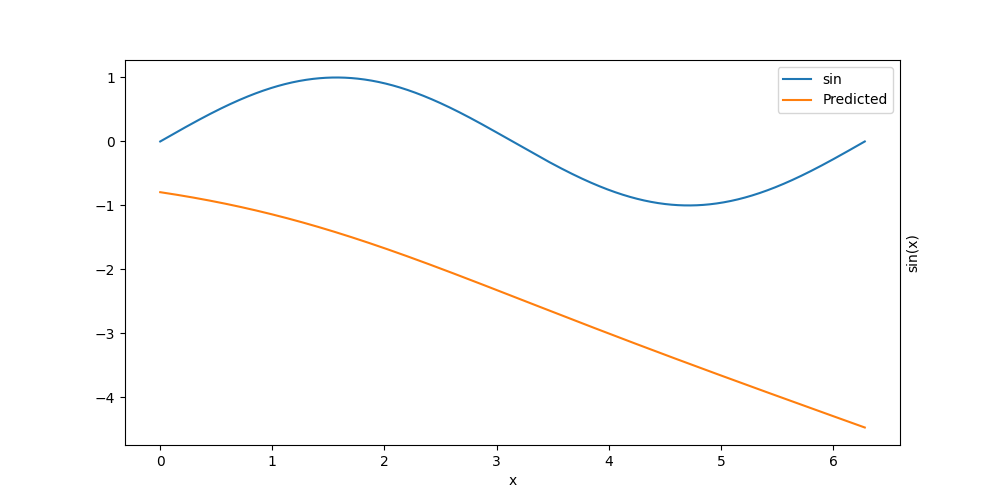
plot tutorial
Initial error: 6.69e+00

Here we guide it a bit in the right direction to make it learn faster

growing_net[0].weight.data = torch.ones_like(growing_net[0].weight.data)
growing_net[0].bias.data = torch.tensor([-2.0, -3 * torch.pi / 2], device=global_device())
growing_net[1].weight.data = torch.tensor([[-1.0, 2.0]], device=global_device())
growing_net[1].bias.data = torch.zeros_like(growing_net[1].bias.data)

l2_err = evaluate_model(growing_net, data, loss_function)[0]
print(f"Error: {l2_err:.2e}")
fig, ax = plt.subplots(1, 1, figsize=(10, 5))
plt_model(growing_net, ax)
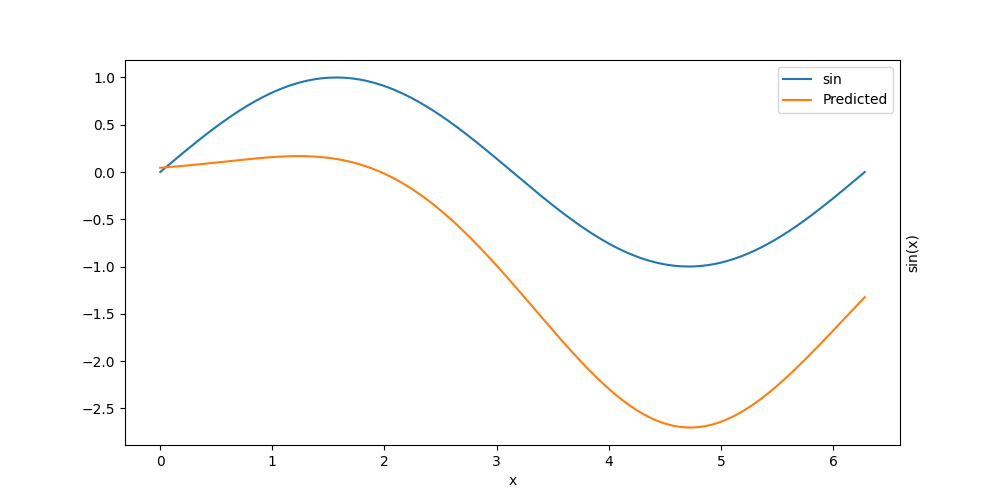
plot tutorial
Error: 1.48e+00

optimizer = torch.optim.SGD(growing_net.parameters(), lr=1e-2)
# optimizer = torch.optim.Adam(net.parameters(), lr=1e-3)

res = train(
    model=growing_net,
    train_dataloader=data,
    optimizer=optimizer,
    nb_epoch=10,
    show=False,
    aux_loss_function=None,
)
loss_train, accuracy_train, loss_val, _ = res
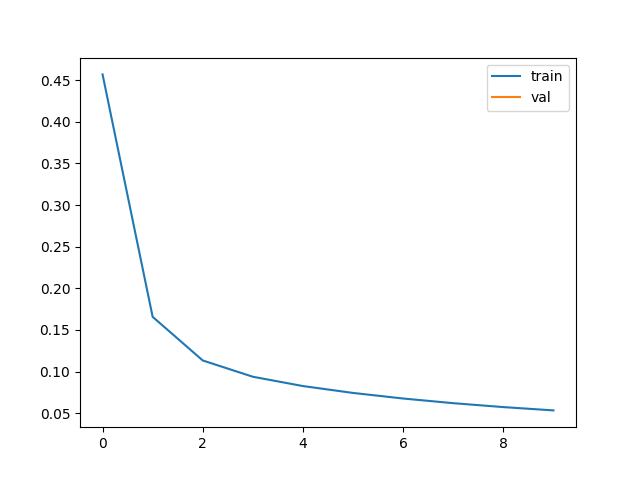
plt.plot(loss_train, label="train")
plt.plot(loss_val, label="val")
plt.legend()
plt.show()

l2_err = evaluate_model(growing_net, data, loss_function, aux_loss_function=None)[0]
print(f"Error: {l2_err:.2e}")
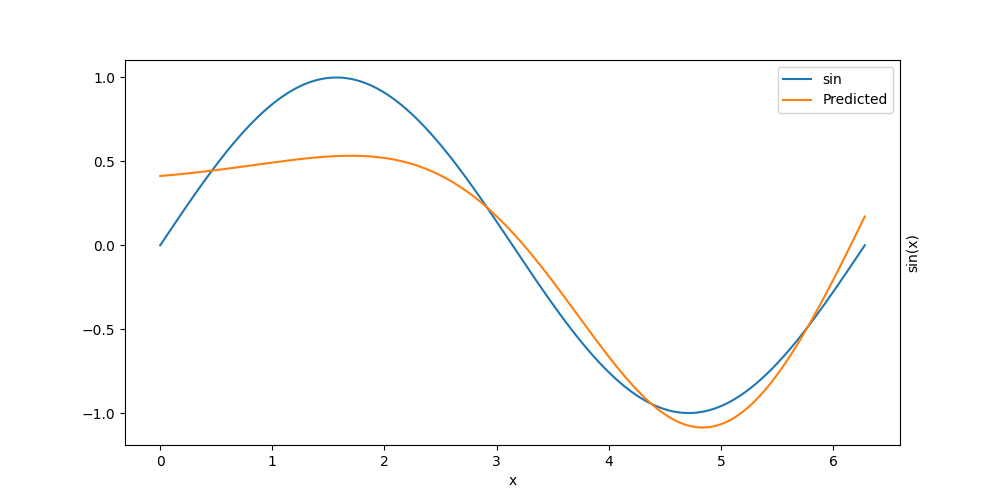
fig, ax = plt.subplots(1, 1, figsize=(10, 5))
plt_model(growing_net, ax)
  • plot tutorial
  • plot tutorial
Error: 5.13e-02

Here with only two hidden neurons, we have a limited expressiveness. Therefore we would like to add new neurons to the model.

3. Prepare the growth#

To add new neurons we need information about the current model. To get those the first set is to initialize the computation of those.

print(growing_net[0].__str__(verbose=2))
print(growing_net[1].__str__(verbose=2))

LinearGrowingModule(first_layer) module with 4 parameters.
        Layer : Linear(in_features=1, out_features=2, bias=True)
        Post layer function : GELU(approximate='none')
        Allow growing : False
        Store input : False
        self._internal_store_input=False
        Store pre-activity : False
        self._internal_store_pre_activity=False
        Tensor S (internal) : S(LinearGrowingModule(first_layer)) tensor of shape (2, 2) with 0 samples
        Tensor S : S(LinearGrowingModule(first_layer)) tensor of shape (2, 2) with 0 samples
        Tensor M : M(LinearGrowingModule(first_layer)) tensor of shape (2, 2) with 0 samples
        Optimal delta layer : None
        Extended input layer : None
        Extended output layer : None
LinearGrowingModule(second_layer) module with 3 parameters.
        Layer : Linear(in_features=2, out_features=1, bias=True)
        Post layer function : Identity()
        Allow growing : False
        Store input : False
        self._internal_store_input=False
        Store pre-activity : False
        self._internal_store_pre_activity=False
        Tensor S (internal) : S(LinearGrowingModule(second_layer)) tensor of shape (3, 3) with 0 samples
        Tensor S : S(LinearGrowingModule(second_layer)) tensor of shape (3, 3) with 0 samples
        Tensor M : M(LinearGrowingModule(second_layer)) tensor of shape (3, 1) with 0 samples
        Optimal delta layer : None
        Extended input layer : None
        Extended output layer : None

Above you can see that nothing is stored in the model.

growing_net[1].init_computation()

print(growing_net[0].__str__(verbose=2))
print(growing_net[1].__str__(verbose=2))

LinearGrowingModule(first_layer) module with 4 parameters.
        Layer : Linear(in_features=1, out_features=2, bias=True)
        Post layer function : GELU(approximate='none')
        Allow growing : False
        Store input : True
        self._internal_store_input=True
        Store pre-activity : False
        self._internal_store_pre_activity=False
        Tensor S (internal) : S(LinearGrowingModule(first_layer)) tensor of shape (2, 2) with 0 samples
        Tensor S : S(LinearGrowingModule(first_layer)) tensor of shape (2, 2) with 0 samples
        Tensor M : M(LinearGrowingModule(first_layer)) tensor of shape (2, 2) with 0 samples
        Optimal delta layer : None
        Extended input layer : None
        Extended output layer : None
LinearGrowingModule(second_layer) module with 3 parameters.
        Layer : Linear(in_features=2, out_features=1, bias=True)
        Post layer function : Identity()
        Allow growing : False
        Store input : True
        self._internal_store_input=True
        Store pre-activity : True
        self._internal_store_pre_activity=True
        Tensor S (internal) : S(LinearGrowingModule(second_layer)) tensor of shape (3, 3) with 0 samples
        Tensor S : S(LinearGrowingModule(second_layer)) tensor of shape (3, 3) with 0 samples
        Tensor M : M(LinearGrowingModule(second_layer)) tensor of shape (3, 1) with 0 samples
        Optimal delta layer : None
        Extended input layer : None
        Extended output layer : None

Above you can see that one the computation are initialised, we see that Store input : True. This means that the next time we forward through the graph we will store the input of the layers for which store_input=True.

We then do the forward/backward pass to compute all the raw information needed, then we call update_computation to aggregate the raw informatons into statistics like the tensors S and M.

# Here we switch to a sum loss function !
# This is important as we already make the average internally
loss_sum = torch.nn.MSELoss(reduction="sum")

for x, sinx in data:
    out = growing_net(x)

    error = loss_sum(out, sinx)
    error.backward()

    growing_net[1].update_computation()

Below you can see that indeed Tensor S and Tensor M are now estimated over 1000 samples.

print(growing_net[0].__str__(verbose=2))
print(growing_net[1].__str__(verbose=2))

LinearGrowingModule(first_layer) module with 4 parameters.
        Layer : Linear(in_features=1, out_features=2, bias=True)
        Post layer function : GELU(approximate='none')
        Allow growing : False
        Store input : True
        self._internal_store_input=True
        Store pre-activity : False
        self._internal_store_pre_activity=False
        Tensor S (internal) : S(LinearGrowingModule(first_layer)) tensor of shape (2, 2) with 1000 samples
        Tensor S : S(LinearGrowingModule(first_layer)) tensor of shape (2, 2) with 1000 samples
        Tensor M : M(LinearGrowingModule(first_layer)) tensor of shape (2, 2) with 0 samples
        Optimal delta layer : None
        Extended input layer : None
        Extended output layer : None
LinearGrowingModule(second_layer) module with 3 parameters.
        Layer : Linear(in_features=2, out_features=1, bias=True)
        Post layer function : Identity()
        Allow growing : False
        Store input : True
        self._internal_store_input=True
        Store pre-activity : True
        self._internal_store_pre_activity=True
        Tensor S (internal) : S(LinearGrowingModule(second_layer)) tensor of shape (3, 3) with 1000 samples
        Tensor S : S(LinearGrowingModule(second_layer)) tensor of shape (3, 3) with 1000 samples
        Tensor M : M(LinearGrowingModule(second_layer)) tensor of shape (3, 1) with 1000 samples
        Optimal delta layer : None
        Extended input layer : None
        Extended output layer : None

Then we can compute the natural gradient step and the new neurons to add with compute_optimal_updates. You can see that now the first layer store an extended output layer that will compute the new values of the neurons. The second layer has also been extended with an extended input layer. In addition the second layer has a Optimal delta layer which correspond to the natural gradient step.

growing_net[1].compute_optimal_updates()
print(growing_net[0].__str__(verbose=2))
print(growing_net[1].__str__(verbose=2))

LinearGrowingModule(first_layer) module with 4 parameters.
        Layer : Linear(in_features=1, out_features=2, bias=True)
        Post layer function : GELU(approximate='none')
        Allow growing : False
        Store input : True
        self._internal_store_input=True
        Store pre-activity : False
        self._internal_store_pre_activity=False
        Tensor S (internal) : S(LinearGrowingModule(first_layer)) tensor of shape (2, 2) with 1000 samples
        Tensor S : S(LinearGrowingModule(first_layer)) tensor of shape (2, 2) with 1000 samples
        Tensor M : M(LinearGrowingModule(first_layer)) tensor of shape (2, 2) with 0 samples
        Optimal delta layer : None
        Extended input layer : None
        Extended output layer : Linear(in_features=1, out_features=1, bias=True)
LinearGrowingModule(second_layer) module with 3 parameters.
        Layer : Linear(in_features=2, out_features=1, bias=True)
        Post layer function : Identity()
        Allow growing : False
        Store input : True
        self._internal_store_input=True
        Store pre-activity : True
        self._internal_store_pre_activity=True
        Tensor S (internal) : S(LinearGrowingModule(second_layer)) tensor of shape (3, 3) with 1000 samples
        Tensor S : S(LinearGrowingModule(second_layer)) tensor of shape (3, 3) with 1000 samples
        Tensor M : M(LinearGrowingModule(second_layer)) tensor of shape (3, 1) with 1000 samples
        Optimal delta layer : Linear(in_features=2, out_features=1, bias=True)
        Extended input layer : Linear(in_features=1, out_features=1, bias=True)
        Extended output layer : None

Once the updates are computed we can stop computing statistics and storing them. This is done by calling the reset_computation method.

growing_net[1].reset_computation()
print(growing_net[0].__str__(verbose=2))
print(growing_net[1].__str__(verbose=2))

LinearGrowingModule(first_layer) module with 4 parameters.
        Layer : Linear(in_features=1, out_features=2, bias=True)
        Post layer function : GELU(approximate='none')
        Allow growing : False
        Store input : True
        self._internal_store_input=True
        Store pre-activity : False
        self._internal_store_pre_activity=False
        Tensor S (internal) : S(LinearGrowingModule(first_layer)) tensor of shape (2, 2) with 0 samples
        Tensor S : S(LinearGrowingModule(first_layer)) tensor of shape (2, 2) with 0 samples
        Tensor M : M(LinearGrowingModule(first_layer)) tensor of shape (2, 2) with 0 samples
        Optimal delta layer : None
        Extended input layer : None
        Extended output layer : Linear(in_features=1, out_features=1, bias=True)
LinearGrowingModule(second_layer) module with 3 parameters.
        Layer : Linear(in_features=2, out_features=1, bias=True)
        Post layer function : Identity()
        Allow growing : False
        Store input : False
        self._internal_store_input=False
        Store pre-activity : False
        self._internal_store_pre_activity=False
        Tensor S (internal) : S(LinearGrowingModule(second_layer)) tensor of shape (3, 3) with 0 samples
        Tensor S : S(LinearGrowingModule(second_layer)) tensor of shape (3, 3) with 0 samples
        Tensor M : M(LinearGrowingModule(second_layer)) tensor of shape (3, 1) with 0 samples
        Optimal delta layer : Linear(in_features=2, out_features=1, bias=True)
        Extended input layer : Linear(in_features=1, out_features=1, bias=True)
        Extended output layer : None

Here we can see that the first layer still store the input. To correct it we can simply set store_input=False in the first layer.

growing_net[0].store_input = False
print(growing_net[0].__str__(verbose=2))
print(growing_net[1].__str__(verbose=2))

LinearGrowingModule(first_layer) module with 4 parameters.
        Layer : Linear(in_features=1, out_features=2, bias=True)
        Post layer function : GELU(approximate='none')
        Allow growing : False
        Store input : False
        self._internal_store_input=False
        Store pre-activity : False
        self._internal_store_pre_activity=False
        Tensor S (internal) : S(LinearGrowingModule(first_layer)) tensor of shape (2, 2) with 0 samples
        Tensor S : S(LinearGrowingModule(first_layer)) tensor of shape (2, 2) with 0 samples
        Tensor M : M(LinearGrowingModule(first_layer)) tensor of shape (2, 2) with 0 samples
        Optimal delta layer : None
        Extended input layer : None
        Extended output layer : Linear(in_features=1, out_features=1, bias=True)
LinearGrowingModule(second_layer) module with 3 parameters.
        Layer : Linear(in_features=2, out_features=1, bias=True)
        Post layer function : Identity()
        Allow growing : False
        Store input : False
        self._internal_store_input=False
        Store pre-activity : False
        self._internal_store_pre_activity=False
        Tensor S (internal) : S(LinearGrowingModule(second_layer)) tensor of shape (3, 3) with 0 samples
        Tensor S : S(LinearGrowingModule(second_layer)) tensor of shape (3, 3) with 0 samples
        Tensor M : M(LinearGrowingModule(second_layer)) tensor of shape (3, 1) with 0 samples
        Optimal delta layer : Linear(in_features=2, out_features=1, bias=True)
        Extended input layer : Linear(in_features=1, out_features=1, bias=True)
        Extended output layer : None

4. Choose a scaling factor#

Once we computed the updates we can choose a scaling factor. This scaling factor \(\gamma\) will scale the updates by \(\gamma\) when they have a quadratic effect (like the new incoming and outgoing weights) or \(\gamma^2\) when they have a linear effect (like the natural gradient step).

growing_net[1].scaling_factor = 0.5

def extended_evaluate_model(
    growing_model: torch.nn.Sequential,
    dataloader: torch.utils.data.DataLoader,
    loss_function: torch.nn.Module = torch.nn.MSELoss(reduction="sum"),
    batch_limit: int = -1,
    device: torch.device = global_device(),
) -> float:
    assert (
        loss_function.reduction == "sum"
    ), "The loss function should not be averaged over the batch"
    growing_model.eval()
    n_batch = 0
    nb_sample = 0
    total_loss = torch.tensor(0.0, device=device)
    for x, y in dataloader:
        growing_model.zero_grad()
        x, y = x.to(device), y.to(device)
        z, z_ext = growing_model[0].extended_forward(x)
        y_pred, _ = growing_model[1].extended_forward(z, z_ext)
        loss = loss_function(y_pred, y)
        total_loss += loss
        nb_sample += x.size(0)
        n_batch += 1
        if 0 <= batch_limit <= n_batch:
            break
    return total_loss.item() / nb_sample

We can use a special forward extended_forward that takes into account the proposed modification of the network to evaluate their effect on the loss.

new_error = extended_evaluate_model(
    growing_net,
    data,
    loss_sum,
)

print(f"New error: {new_error:.2e}")

New error: 3.81e-02

5. Apply the changes#

Once we have chosen a scaling factor we can apply the changes to the model. This is done by calling the apply_change methods.

growing_net[1].apply_change()
print(growing_net[0].__str__(verbose=2))
print(growing_net[1].__str__(verbose=2))

LinearGrowingModule(first_layer) module with 6 parameters.
        Layer : Linear(in_features=1, out_features=3, bias=True)
        Post layer function : GELU(approximate='none')
        Allow growing : False
        Store input : False
        self._internal_store_input=False
        Store pre-activity : False
        self._internal_store_pre_activity=False
        Tensor S (internal) : S(LinearGrowingModule(first_layer)) tensor of shape (2, 2) with 0 samples
        Tensor S : S(LinearGrowingModule(first_layer)) tensor of shape (2, 2) with 0 samples
        Tensor M : M(LinearGrowingModule(first_layer)) tensor of shape (2, 3) with 0 samples
        Optimal delta layer : None
        Extended input layer : None
        Extended output layer : Linear(in_features=1, out_features=1, bias=True)
LinearGrowingModule(second_layer) module with 4 parameters.
        Layer : Linear(in_features=3, out_features=1, bias=True)
        Post layer function : Identity()
        Allow growing : False
        Store input : False
        self._internal_store_input=False
        Store pre-activity : False
        self._internal_store_pre_activity=False
        Tensor S (internal) : S(LinearGrowingModule(second_layer)) tensor of shape (4, 4) with 0 samples
        Tensor S : S(LinearGrowingModule(second_layer)) tensor of shape (4, 4) with 0 samples
        Tensor M : M(LinearGrowingModule(second_layer)) tensor of shape (4, 1) with 0 samples
        Optimal delta layer : Linear(in_features=2, out_features=1, bias=True)
        Extended input layer : Linear(in_features=1, out_features=1, bias=True)
        Extended output layer : None

We can then delete the extended_output_layer, extended_input_layer and Optimal delta layer as they are not needed anymore.

growing_net[1].delete_update()
print(growing_net[0].__str__(verbose=2))
print(growing_net[1].__str__(verbose=2))

LinearGrowingModule(first_layer) module with 6 parameters.
        Layer : Linear(in_features=1, out_features=3, bias=True)
        Post layer function : GELU(approximate='none')
        Allow growing : False
        Store input : False
        self._internal_store_input=False
        Store pre-activity : False
        self._internal_store_pre_activity=False
        Tensor S (internal) : S(LinearGrowingModule(first_layer)) tensor of shape (2, 2) with 0 samples
        Tensor S : S(LinearGrowingModule(first_layer)) tensor of shape (2, 2) with 0 samples
        Tensor M : M(LinearGrowingModule(first_layer)) tensor of shape (2, 3) with 0 samples
        Optimal delta layer : None
        Extended input layer : None
        Extended output layer : None
LinearGrowingModule(second_layer) module with 4 parameters.
        Layer : Linear(in_features=3, out_features=1, bias=True)
        Post layer function : Identity()
        Allow growing : False
        Store input : False
        self._internal_store_input=False
        Store pre-activity : False
        self._internal_store_pre_activity=False
        Tensor S (internal) : S(LinearGrowingModule(second_layer)) tensor of shape (4, 4) with 0 samples
        Tensor S : S(LinearGrowingModule(second_layer)) tensor of shape (4, 4) with 0 samples
        Tensor M : M(LinearGrowingModule(second_layer)) tensor of shape (4, 1) with 0 samples
        Optimal delta layer : None
        Extended input layer : None
        Extended output layer : None

6. Use your grown model#

You then get a fully working model that can be used like a normal PyTorch model. You can train it, evaluate it, etc.

l2_err = evaluate_model(growing_net, data, loss_function)[0]
print(f"New error: {l2_err:.2e}")
fig, ax = plt.subplots(1, 1, figsize=(10, 5))
plt_model(growing_net, ax)
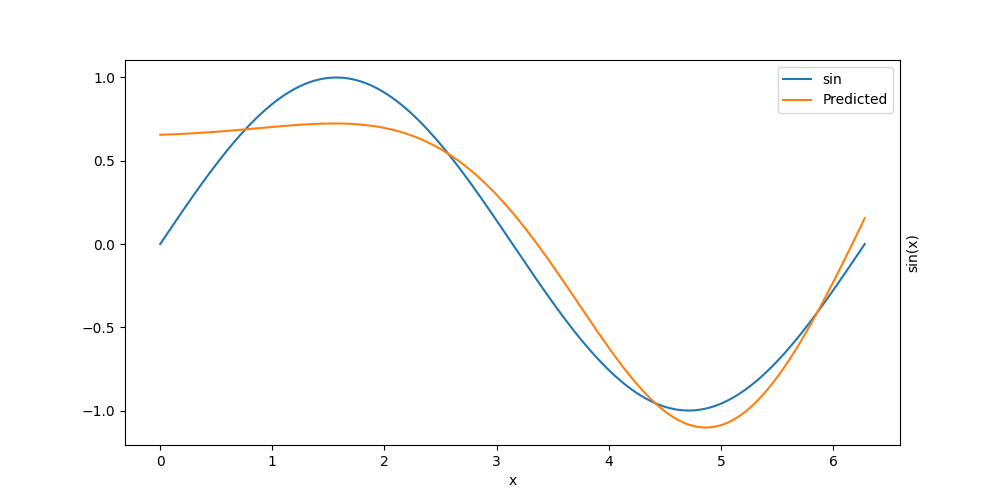
plot tutorial
New error: 3.81e-02

print(growing_net[0].__str__(verbose=2))
print(growing_net[1].__str__(verbose=2))

LinearGrowingModule(first_layer) module with 6 parameters.
        Layer : Linear(in_features=1, out_features=3, bias=True)
        Post layer function : GELU(approximate='none')
        Allow growing : False
        Store input : False
        self._internal_store_input=False
        Store pre-activity : False
        self._internal_store_pre_activity=False
        Tensor S (internal) : S(LinearGrowingModule(first_layer)) tensor of shape (2, 2) with 0 samples
        Tensor S : S(LinearGrowingModule(first_layer)) tensor of shape (2, 2) with 0 samples
        Tensor M : M(LinearGrowingModule(first_layer)) tensor of shape (2, 3) with 0 samples
        Optimal delta layer : None
        Extended input layer : None
        Extended output layer : None
LinearGrowingModule(second_layer) module with 4 parameters.
        Layer : Linear(in_features=3, out_features=1, bias=True)
        Post layer function : Identity()
        Allow growing : False
        Store input : False
        self._internal_store_input=False
        Store pre-activity : False
        self._internal_store_pre_activity=False
        Tensor S (internal) : S(LinearGrowingModule(second_layer)) tensor of shape (4, 4) with 0 samples
        Tensor S : S(LinearGrowingModule(second_layer)) tensor of shape (4, 4) with 0 samples
        Tensor M : M(LinearGrowingModule(second_layer)) tensor of shape (4, 1) with 0 samples
        Optimal delta layer : None
        Extended input layer : None
        Extended output layer : None

Total running time of the script: (0 minutes 0.390 seconds)

Gallery generated by Sphinx-Gallery